4 Position and Direction Vectors

4 Position and Direction Vectors🔗ℹ

A vector in 3D space is uniquely identified by three real numbers called coordinates or components. For example, the coordinates of (pos 1 2 3) are 1, 2 and 3.

Pict3D distinguishes between two kinds of vectors:

A position vector, which is a value of type Pos, represents an absolute position in 3D space.
A direction vector, which is a value of type Dir, represents a direction, with distance, in 3D space.

Generally, think of direction vectors as how to get from one position vector in space to another.

Suppose we define a direction vector dv1 as

> (define dv1 (dir 1 1 0))

To picture it, we need a starting position vector. We’ll arbitrarily choose the origin, which is (pos 0 0 0).

> (define v origin)
> (arrow v dv1)

We can use the direction vector dv1 to move the center of a sphere.

> (define move-once
    (combine (arrow v dv1)
             (sphere v 0.1)
             (sphere (pos+ v dv1) 0.1)))
> move-once

We might even define another direction vector dv2 (pointing upward) to move it again.

> (define dv2 (dir 0 0 1))
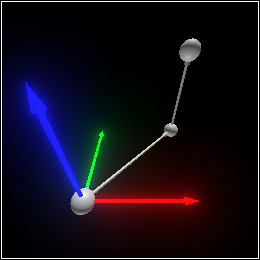
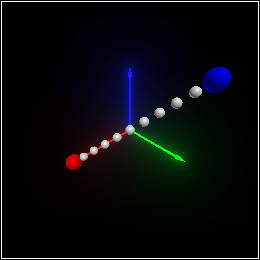
> (define move-twice
    (combine move-once
             (arrow (pos+ v dv1) dv2)
             (sphere (pos+ (pos+ v dv1) dv2) 0.1)))
> move-twice

But we don’t have to move it twice: we can move it just once, by adding the direction vectors dv1 and dv2.

> (define dv (dir+ dv1 dv2))
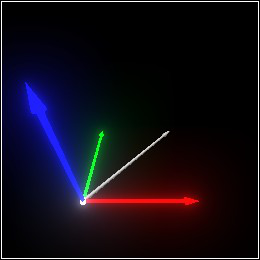
> (define move-twice-by-moving-once
    (combine (arrow v dv)
             (sphere v 0.1)
             (sphere (pos+ v dv) 0.1)))
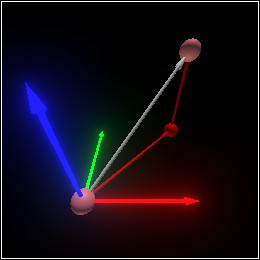
> (combine move-twice-by-moving-once
           (set-color move-twice (rgba "red" 0.75)))

Composing transformations—not just movement, but all parallel-line-preserving transformations—is discussed in the section Transformation.

Directions are used to move entire scenes, not just points:

> (move (combine (with-color (rgba "red" 0.5)
                   (cube origin 1/3))
                 (sphere origin 0.05))
        (dir 1/2 1/2 0))

When used as scaling factors, as in (rectangle origin (dir 1/3 1/3 1)), directions represent moving the center to a corner:

> (move (combine (with-color (rgba "red" 0.5)
                   (rectangle origin (dir 1/3 1/3 1)))
                 (sphere origin 0.05)
                 (arrow origin (dir 1/3 1/3 1)))
        (dir 1/2 1/2 0))

4.1 Direction Vectors🔗ℹ

type
Dir
predicate
dir? : (-> Any Boolean : Dir)

The type and predicate of direction vectors.

procedure
(dir v) → Dir
  v : (U FlVector (Listof Real) (Vectorof Real))
(dir dx dy dz) → Dir
  dx : Real
  dy : Real
  dz : Real

Constructs a direction vector from its components dx, dy and dz, or converts a vector v in another representation to a direction vector.

value
zero-dir : Dir = (dir 0 0 0)

The zero direction. Analogous to origin.

value
+x : Dir = (dir  1  0  0)
value
-x : Dir = (dir -1  0  0)
value
+y : Dir = (dir  0  1  0)
value
-y : Dir = (dir  0 -1  0)
value
+z : Dir = (dir  0  0  1)
value
-z : Dir = (dir  0  0 -1)

The positive and negative coordinate axis directions.

Example:

> (with-color (rgba "black")
    (combine (with-emitted (emitted "cyan" 2)
               (arrow origin -x))
             (with-emitted (emitted "magenta" 2)
               (arrow origin -y))
             (with-emitted (emitted "yellow" 2)
               (arrow origin -z))))

Alternatively, these are the face normals for an axis-aligned rectangle, or the directions from the center of a (cube v 1) to the centers of each of its faces.

value
+x+y : Dir = (dir  1  1  0)
value
+x-y : Dir = (dir  1 -1  0)
value
+y+z : Dir = (dir  0  1  1)
value
+y-z : Dir = (dir  0  1 -1)
value
+x+z : Dir = (dir  1  0  1)
value
+x-z : Dir = (dir  1  0 -1)
value
-x+y : Dir = (dir -1  1  0)
value
-x-y : Dir = (dir -1 -1  0)
value
-y+z : Dir = (dir  0 -1  1)
value
-y-z : Dir = (dir  0 -1 -1)
value
-x+z : Dir = (dir -1  0  1)
value
-x-z : Dir = (dir -1  0 -1)

The directions from the center of a (cube v 1) to the centers of each of its edges.

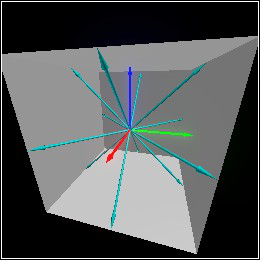
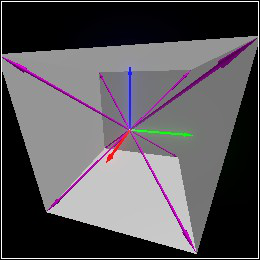
> (combine
   (cube origin 1 #:inside? #t)
   (with-color (rgba "cyan")
     (for/list ([dv  (list +x+y +x-y +y+z +y-z +x+z +x-z
                           -x+y -x-y -y+z -y-z -x+z -x-z)])
       (arrow origin dv)))
   (basis 'camera (point-at (pos 2 0.5 0.75) origin)))

value
+x+y+z : Dir = (dir  1  1  1)
value
+x+y-z : Dir = (dir  1  1 -1)
value
+x-y+z : Dir = (dir  1 -1  1)
value
+x-y-z : Dir = (dir  1 -1 -1)
value
-x+y+z : Dir = (dir -1  1  1)
value
-x+y-z : Dir = (dir -1  1 -1)
value
-x-y+z : Dir = (dir -1 -1  1)
value
-x-y-z : Dir = (dir -1 -1 -1)

The directions from the center of a (cube v 1) to each of its corners.

> (combine
   (cube origin 1 #:inside? #t)
   (with-color (rgba "magenta")
     (for/list ([dv  (list +x+y+z +x+y-z +x-y+z +x-y-z
                           -x+y+z -x+y-z -x-y+z -x-y-z)])
       (arrow origin dv)))
   (basis 'camera (point-at (pos 2 0.5 0.75) origin)))

procedure
(dir+ dv1 dv2) → Dir
  dv1 : Dir
  dv2 : Dir
procedure
(dir-scale dv s) → Dir
  dv : Dir
  s : Real
procedure
(dir-negate dv) → Dir
  dv : Dir
procedure
(dir- dv1 dv2) → Dir
  dv1 : Dir
  dv2 : Dir

(dir+ dv1 dv2) composes movement in the directions dv1 and dv2 by adding their components.

(dir-scale dv s) scales the direction dv by multiplying each component by s.

(dir-negate dv) returns the direction opposite dv by negating each component, and is equivalent to (dir-scale dv -1).

(dir- dv1 dv2) is equivalent to (dir+ dv1 (dir-negate dv2)).

procedure
(dir-dist dv) → Flonum
dv : Dir
procedure
(dir-dist^2 dv) → Flonum
dv : Dir

Return the distance and squared distance represented by dv.

procedure
(dir-norm dv p) → Flonum
dv : Dir
p : Nonnegative-Real

Return the distance represented by dv under the L-p norm.

procedure
(dir-normalize dv) → (U #f Dir)
dv : Dir

Returns a new direction vector in the same direction as dv, but distance 1. If dv is (dir 0 0 0), (dir-normalize dv) returns #f.

procedure
(dir-dot dv1 dv2) → Flonum
dv1 : Dir
dv2 : Dir

Returns the dot product of dv1 and dv2.

procedure
(dir-cross dv1 dv2) → Dir
dv1 : Dir
dv2 : Dir

Returns the cross product of dv1 and dv2.

procedure
(dir-project dv1 dv2) → (U #f Dir)
dv1 : Dir
dv2 : Dir

Returns the projection of dv1 onto dv2, or #f if dv2 is (dir 0 0 0).

procedure
(dir-reject dv1 dv2 [s]) → Dir
  dv1 : Dir
  dv2 : Dir
  s : Real = 1

Returns the rejection of dv1 from dv2. Equivalent to

(dir- dv1 (dir-scale (dir-project dv1 dv2) s))

when (dir-project dv1 dv2) doesn’t return #f.

procedure
(dir-reflect dv1 dv2) → Dir
dv1 : Dir
dv2 : Dir

Reflects dv1 in the direction dv2. Equivalent to (dir-reject dv1 dv2 2).

If dv is the velocity of an object that hits an immovable surface with normal n, then (dir-reject dv n) is the object’s new velocity, assuming an ideal elastic collision.

In other words, use this function to bounce things off walls in games.

procedure
(angles->dir yaw pitch) → Dir
yaw : Real
pitch : Real

Converts yaw (aka longitude, or rotation about the z axis) and pitch (aka latitude, or rotation about the x axis) into a direction with distance 1. Both angles are measured in degrees. Yaw is applied first.

procedure
(dir->angles dv) → (Values Flonum Flonum)
dv : Dir

Converts a direction dv into yaw (aka longitude) and pitch (aka latitude). This is the inverse of angles->dir.

procedure
(dir-dx dv) → Flonum
  dv : Dir
procedure
(dir-dy dv) → Flonum
  dv : Dir
procedure
(dir-dz dv) → Flonum
  dv : Dir

Return the components of dv.

You’ll usually want to use match or match-define instead:

> (match-define (dir dx dy dz) (dir 1 2 3))
> (list dx dy dz)
'(1.0 2.0 3.0)

4.2 Position Vectors🔗ℹ

type
Pos
predicate
pos? : (-> Any Boolean : Pos)

The type and predicate of position vectors.

procedure
(pos v) → Pos
  v : (U FlVector (Listof Real) (Vectorof Real))
(pos x y z) → Pos
  x : Real
  y : Real
  z : Real

Constructs a position vector from its coordinates x, y and z, or converts a vector v in another representation to a position vector.

value
origin : Pos = (pos 0 0 0)

The origin. If 3D space has a center, this is it. Analogous to zero-dir.

procedure
(pos+ v dv [s]) → Pos
  v : Pos
  dv : Dir
  s : Real = 1.0

Moves v in direction dv optionally scaled by s. (pos+ v dv s) is equivalent to (pos+ v (dir-scale dv s)), but more accurate when one of the resulting components is near 0.0.

procedure
(pos- end start) → Dir
end : Pos
start : Pos

Returns the direction to move in to get from start to end; i.e. the dv for which (pos+ start dv) is end.

procedure
(pos-between start end t) → Pos
  start : Pos
  end : Pos
  t : Real

Interpolates between start and end by fraction t. The fraction t should be between 0 and 1, but does not have to be.

Example:

> (combine
   (with-color (rgba "red")
     (sphere (pos 1 0 0) 1/10))
   (with-color (rgba "blue")
     (sphere (pos 0 1 1) 1/10))
   (for/list ([t  (in-range 1/10 1 1/10)])
     (define v (pos-between (pos 1 0 0) (pos 0 1 1) t))
     (sphere v 1/20)))

procedure
(pos-dist v1 v2) → Flonum
  v1 : Pos
  v2 : Pos
procedure
(pos-dist^2 v1 v2) → Flonum
  v1 : Pos
  v2 : Pos

Return the distance and squared distance between v1 and v2.

procedure
(pos-x v) → Flonum
  v : Pos
procedure
(pos-y v) → Flonum
  v : Pos
procedure
(pos-z v) → Flonum
  v : Pos

Return the coordinates of v.

You’ll usually want to use match or match-define instead:

> (match-define (pos x y z) (pos 1 2 3))
> (list x y z)
'(1.0 2.0 3.0)

1	Quick Start
2	Constructors
3	Shape Attributes
4	Position and Direction Vectors
5	Combining Scenes
6	Transformation
7	Deformation and Tessellation
8	Collision Detection
9	Rendering
10	3D Universe