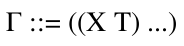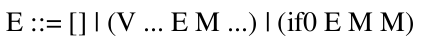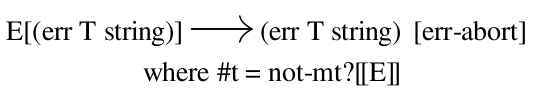From Redex Models to Programming Languages🔗ℹ

David Van Horn <dvanhorn@cs.umd.edu>

1 Overview🔗ℹ

Racket is not merely a programming language–it is a programming language for making programming languages. There are several features that make Racket unique in its ability to support the creation of new languages, but in this article we’re going to look at how to combine two of them—Redex, a domain-specific language for writing mathematical models of programming languages, and the #lang mechanism for creating new programming languages in which Racket modules can be written. In the end, this provides a method for developing programming language models in to fully featured #lang languages integrated into the Racket ecosystem.

2 A Redex Model of PCF🔗ℹ

Let’s start by building a model of a very simple, typed functional programming language based on Plotkin’s PCF language [PCF]. Although simple, PCF contains all the essential elements of a real programming language. Scaling the approach of these notes up to a more sophisticated language is just a small matter of semantic hacking.

2.1 Syntax🔗ℹ

PCF is a core typed functional programming language. For values, it includes natural numbers, functions, and primitive operations. Expressions include conditions, applications, recursive binding, and errors. The syntax of PCF is given in figure 1.

Figure 1: The PCF-source language

For more on using Redex, see the book Semantics Engineering with PLT Redex [Redex].

To model this language in Redex, we first need to define the grammar of the language:

#lang racket

(require redex/reduction-semantics)

(define-language PCF-source

;; Types

(T ::= nat (T ... -> T))

;; Terms

(M ::= X V (M M ...) (μ (X : T) S) (if0 M M M) (err T string))

;; Values

(V ::= N O (λ ([X : T] ...) M))

;; Simple terms

(S ::= V X)

;; Naturals

(N ::= natural)

;; Primitive operations

(O ::= add1 sub1 * + quotient)

;; Variables

(X ::= variable-not-otherwise-mentioned))

It is no accident that the above definition and that of figure 1 look similiar. In fact, typeset grammar of figure 1 is computed from the definition of PCF-source. You can try it for yourself after requiring the redex/pict module:

> (require redex/pict)

> (render-language PCF-source)

At this point, it’s possible to construct PCF programs using Redex’s term constructor. For example, (term (add1 7)) represents the program 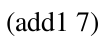. Terms are just s-expression values in Racket:

> (term (add1 7))

'(add1 7)

In order to compute with terms, we need to endow our model with metafunctions, judgments, and relations. So let’s start with a judgment about the syntactic correctness of programs, i.e. let’s start by defining what it means for a term to be well-typed.

Figure 2: Typing judgment typeof (selected cases)

This judgment relies on a type environment, Γ, which not included in the PCF-source definition. To define type environments, we add a definition to PCF-source, shown in figure 3.

Figure 3: Type environments

The code for the typing judgment takes the following form:

(define-judgment-form PCF-source

#:mode (typeof I I O)

#:contract (typeof Γ M T)

[(typeof Γ (err T string) T)]

[(typeof Γ N nat)]

...)

The rest is straightforward to transliterate from figure 2. As you’ll notice, there are two cases that rely on a metafunction extend to extend the type environment. You should be able to write this and the remaining cases of typeof as an exercise.

The #:mode and #:contract specifications says this judgment takes the environment and term as inputs, and produces a type as an output. The judgment is really a relation that has been inductively defined. Since in general a relation may relate several ouputs to a single input, the judgment can also be seen as a function from inputs to sets of outputs. To check whether the judgment holds for specific inputs and outputs, we can query the relation to ask if the inputs and outputs are related:

> (judgment-holds (typeof () 7 nat))

#t

> (judgment-holds (typeof ((f (nat -> nat))) (f 7) nat))

#t

> (judgment-holds (typeof () (7 add1) nat))

#f

It’s also possible to write patterns for the outputs and compute a set of outputs rather than check if a particular one is in the relation:

> (judgment-holds (typeof () 7 T) T)

'(nat)

> (judgment-holds (typeof ((f (nat -> nat))) (f 7) T) T)

'(nat)

> (judgment-holds (typeof () (7 add1) T) T)

'()

(If you think about it, you can probably convince yourself that typeof relates programs to at most one type. What does that mean about the typeof relation? Try to come up with some judgment that relates inputs to multiple outputs and experiment with it.)

Now that we have the syntax and type judgment defined, let’s move on to the dynamic semantics of PCF.

2.2 Semantics🔗ℹ

The semantics of PCF is given by a reduction relation which is relation on program text that transforms a fragment of text into a simpler expression. You should think of this relation as specifying a kind of algebra of PCF programs: you can simplyify programs in the same way you can simplify arithmetic expressions, but instead of appealing to just the axioms of arithmetic, there are axioms for function application, conditionals, and recursion, etc. These axioms are shown in figure 4.

Figure 4: Reduction relation v-source

The v-source relation makes use of three helper metafunctions. The first, subst, does substitution. Rather than define it yourself, you can import this one from pcf/private/subst—or you can look at how to it yourself in the Redex book. It does what you might expect; here it used to substitute 4 and 7 for x and y, respectively, in the expression (term (+ x (* y x))):

> (require pcf/private/subst)

> (term (subst (x 4) (y 7) (+ x (* y x))))

'(+ 4 (* 7 4))

The second metafunction, δ, interprets the application of primitive operations to values. Its definition is fairly straightforward:

(define-metafunction PCF-source

δ : O V ... -> M

[(δ add1 N)           ,(add1 (term N))]

[(δ sub1 N)           ,(max 0 (sub1 (term N)))]

[(δ * N_0 N_1)        ,(* (term N_0) (term N_1))]

[(δ + N_0 N_1)        ,(+ (term N_0) (term N_1))]

[(δ quotient N_0 0)    (err nat "Divide by zero")]

[(δ quotient N_0 N_1) ,(quotient (term N_0) (term N_1))])

Notice how term works like quote, but interprets metafunctions.

The third and final metafunction used by v-source is nonzero?, which by now you should have no problem defining.

Finally, we can now compute with programs by using the reduction relation, which can be applied by using Redex’s apply-reduction-relation:

> (apply-reduction-relation v-source     (term (add1 7)))

'(8)

> (apply-reduction-relation v-source     (term ((λ ([f : (nat -> nat)]) (f 3)) sub1)))

'((sub1 3))

Notice that in the second example, the relation produced (sub1 3), not 2. That’s because apply-reduction-relation produces the set of terms related to the input by exactly one use of v-source. If you’d like to repeatedly apply v-source until the program is in simplest terms, use apply-reduction-relation*:

> (apply-reduction-relation* v-source     (term ((λ ([f : (nat -> nat)]) (f 3)) sub1)))

'(2)

While the v-source relates terms that can immediately be reduced, it doesn’t say anything about terms that contain reducible terms, but themselves are not reducible. For example, (term (sub1 (add1 5))) does not match the left-hand-side of any axiom in v-source. To enable such reduction, we need to specify a grammar of evaluation contexts that specify where a reduction may be applied. Here is a definition of evaluation contexts that gives a left-to-right order of evaluation:

Once we add the definition of evaluation contexts to PCF-source, it is possible to define the contextual closure of v with respect to 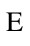, which we call -->v-source:

> (define -->v-source     (context-closure v-source PCF-source E))

> (apply-reduction-relation* -->v-source     (term (sub1 (add1 5))))

'(5)

> (apply-reduction-relation* -->v-source     (term ((μ (fact : (nat -> nat))               (λ ([n : nat])                 (if0 n                      1                      (* n (fact (sub1 n))))))            5)))

'(120)

There is one short-coming of the -->v-source relation that you may have noticed. Programs that produce errors get stuck, e.g.:

> (apply-reduction-relation* -->v-source     (term (sub1 (quotient 5 0))))

'((sub1 (err nat "Divide by zero")))

In this small example, it’s easy to see the program signalled an error, but in anything much larger it becomes very difficult to spot what’s gone wrong when an error is buried deep inside some evaluation context. We can define a reduction relation, err-abort, that handles such situations by discarding the surrounding context and producing the error as the overall result of the computation:

or as code:

> (define err-abort     (reduction-relation      PCF-source #:domain M      (--> (in-hole E (err T string)) (err T string)      (where #t (not-mt? E))      err-abort)))

> (apply-reduction-relation err-abort     (term (sub1 (err nat "Divide by zero"))))

'((err nat "Divide by zero"))

This relation relies on a helper metafunction not-mt? that determines if an evaluation context is not the empty context. (What would happen if you left that side condition off?) Notice how the rule is context-sensitive: it matches the entire program against an evaluation context pattern variable and an error term, then throws the context away on the right-hand-side. To put incorporate this rule into the PCF semantics, let’s re-define -->v-source as the following, which combines the context closure of v-source and the new err-abort relation:

> (define -->v-source     (union-reduction-relations      (context-closure v-source PCF-source E)      err-abort))

Now when an error occurs, it is produced as the result of the computation:

> (apply-reduction-relation* -->v-source     (term (sub1 (quotient 5 0))))

'((err nat "Divide by zero"))

So now we have a working interpreter for PCF in the form of the reflexive, transitive closure of -->v-source, which is exactly what apply-reduction-relation* computes. If we wanted more detail on these computations, we can use some more of the tools that come with Redex. For example, by requiring redex/gui, we can use the traces function for visualizing the trace of computation. For example, the result of

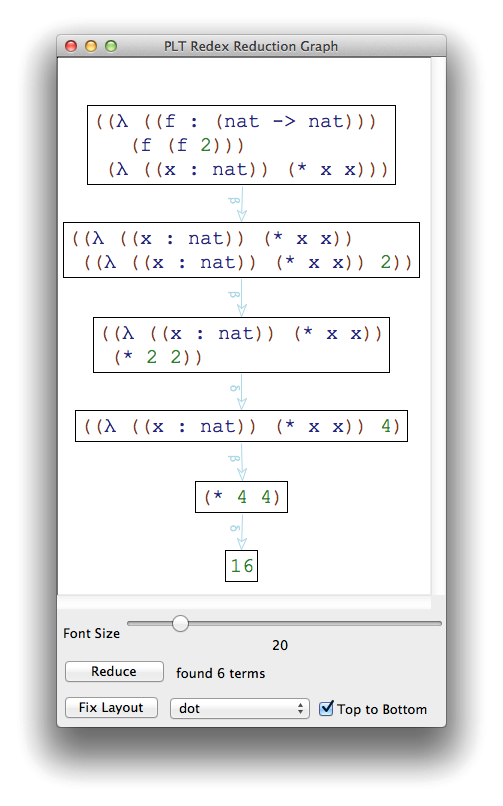
(traces -->v-source

(term ((λ ([f : (nat -> nat)]) (f (f 2)))

(λ ([x : nat]) (* x x)))))

is an interactive window that shows the intermediate terms of the computation as a graph labelled with edges corresponding to reduction axioms, shown in figure 5.

Figure 5: Reduction graph

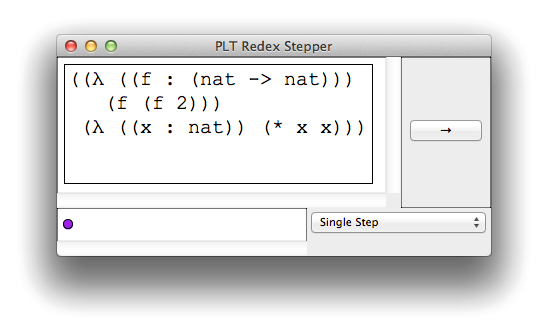
Redex also gives you the ability to step through a computation with an interactive algebraic stepper. Simply use the stepper function:

(stepper -->v-source

(term ((λ ([f : (nat -> nat)]) (f (f 2)))

(λ ([x : nat]) (* x x)))))

which will launch the stepper window shown in figure 6.

Figure 6: Algebraic stepper

At this point, we have the basics of a working model for PCF. We might go further and turn some of our examples into test cases, perhaps state some theorems of PCF and use random testing to try to disprove them, or write a document that uses render-language and friends to typeset the various definitions from our PCF model (a document such as this!).

But the thing we probably won’t be doing a lot of is programming in PCF. It’s just too cumbersome. To write a PCF program you have to load the Redex library and all of the PCF definitions, then you have to use term to construct programs and then use apply-reduction-relation* to compute with them. In other words, we have to embed a PCF program as a datum within a Redex program that interprets it. But Racket makes it easy to go from an interpreter to a #lang language. In the next sections, we’ll explore how to build a #lang for PCF so that it’s just as natural to write PCF programs as it is Racket programs.

3 Building languages🔗ℹ

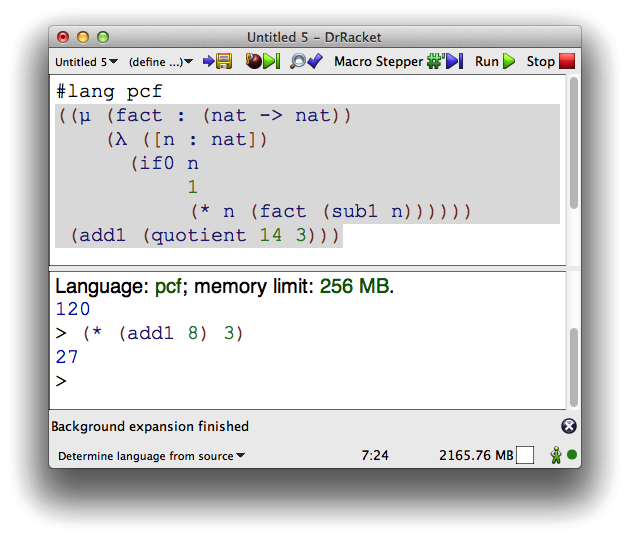
Let’s put the horse before the cart and see the end result of what we’ll accomplish in this section, before seeing how. Our goal is a #lang pcf language that enables us to write PCF programs like this:

In the definitions panel of this DrRacket window, you’ll notice we’ve indicated PCF as the language this module is written in. The subsequent text consists of a PCF expression computing 5!. After pressing “Run”, the interactions panel appears and prints the results from the definitions panel, i.e. 120. After which, we can type PCF expressions at the prompt and get results back interactively.

Not only is it now easier to develop programs written in PCF, it is also easier to discuss PCF programs since we can use the PCF language directly in documenting examples:

> ((μ (fact : (nat -> nat))       (λ ([n : nat])         (if0 n              1              (* n (fact (sub1 n))))))    5)

t: undefined;

cannot reference an identifier before its definition

in module: top-level

It is worth point out that this is a different interaction prompt than the one used before. It is a PCF prompt, not a Racket prompt.

Making a #lang language for an s-expression-based language requires two things:

• a #%module-begin macro that is given programs in the definitions panel as arguments, and

• a #%top-interaction form that is given an expression sent to the interactions panel as an argument.

(If our language’s syntax weren’t based on s-expressions, we’d also have to write a parser.)

We can experiment by defining two macros, pcf-module and pcf-top (we’ve renamed them to the “#%” special names in the provide clause). These macros perform the same basic task, given an expression—or a sequence of expressions in the case of pcf-module— the macro transforms the PCF expression into a Racket expression that evaluates it. So we arrive at the following:

#lang racket

(provide (rename-out [pcf-top #%top-interaction]

[pcf-module #%module-begin]))

(require (for-syntax syntax/parse))

(require redex/reduction-semantics

pcf/source)

(define-syntax (pcf-top stx)

(syntax-parse stx

[(_ . e)

#'(#%top-interaction .

(apply values

(apply-reduction-relation* -->v-source (term e))))]))

(define-syntax (pcf-module stx)

(syntax-parse stx

[(_ e ...)

#'(#%module-begin

(apply values

(append (apply-reduction-relation* -->v-source (term e))

...)))]))

Save the above module in "pcf/source/lang.rkt". At this point, we can write modules in PCF using #lang s-exp pcf/source/lang, but you can make #lang pcf/source available by taking the extra step of creating a file "pcf/source/lang/reader.rkt" with the following contents:

#lang s-exp syntax/module-reader

pcf/source/lang

This is a bit of magic that resides in a specific location that Racket will use to resolve #langs that start with pcf/source. After this, we have a bonafide language:

#lang pcf/source

((μ (fib : (nat -> nat))

(λ ([n : nat])

(if0 n

0

(if0 (sub1 n)

1

(+ (fib (sub1 n))

(fib (sub1 (sub1 n))))))))

5)

One shortcoming of the above code is that type errors are not caught until run-time, and even then, they are “caught” by having the redex model break.

4 Catching type errors with Check Syntax🔗ℹ

One thing you may notice is that Check Syntax does do a whole lot for you, which is really too bad considering Check Syntax now runs continuously in DrRacket. The problem is that the only thing pcf/source does when it is expanded is convert the text from the definitions window into a datum. You can basically write whatever junk you’d like: so long as the parens balance, DrRacket will be perfectly happy with it... until you run it. That’s of course not what DrRacket does for Racket programs. For #lang racket programs, Check Syntax will let you know if you use undefined names, or leave off an else branch in an if. In other words, it’s continuously checking the well-formedness of your program. Wouldn’t it be nice to get some of that chocolate on our peanut-butter?

Well, we have a couple perfectly sensible well-formedness condition on PCF programs. One simple one is just to check that the input follows the grammar of PCF. We can do one better though and further make sure the input is well-typed by using the typeof judgment from the PCF model.

5 Lexical structure🔗ℹ

6 Highlighting run-time errors🔗ℹ

7 Typesetting examples🔗ℹ

As mentioned in Building languages, once we have a #lang language, it becomes possible to use that language just like any other #lang language. For example, in this document, there is a Racket evaluator for showing examples of using Redex, and there is a PCF evaluator for showing examples using PCF. Both are constructed at the beginning of the Scribble document like so:

#lang scribble/manual

@(require racket/sandbox

scribble/eval)

@(define (make-eval . reqs)

(call-with-trusted-sandbox-configuration

(lambda ()

(parameterize ([sandbox-output 'string]

[sandbox-error-output 'string])

(let ([the-eval (make-base-eval)])

(the-eval `(require ,@reqs))

the-eval)))))

@(define pcf-eval (make-eval 'pcf/lang))

@(define redex-eval

(make-eval 'redex/reduction-semantics

'redex/pict

'pcf/source))

at which point it’s easy to write code to typeset examples of either language. For example this:

@(examples #:eval pcf-eval

((μ (fact : (nat -> nat))

(λ ([n : nat])

(if0 n

1

(* n (fact (sub1 n))))))

5))

will create an example that looks like this:

8 Where to Go from Here🔗ℹ

Bibliography🔗ℹ