9.1.0.9
Unstable Flonums: May Change Without Warning
This library is unstable;
compatibility will not be maintained.
See Unstable: May Change Without Warning
for more information.
| (require unstable/flonum) | package: unstable-flonum-lib |
You should almost certainly use math/flonum instead of this module, which is more complete and can be used in Typed Racket code.
procedure
(flonum->bit-field x) → (integer-in 0 (- (expt 2 64) 1))
x : flonum?
Returns the bits comprising x as an integer.
A convenient shortcut for composing integer-bytes->integer with real->floating-point-bytes.
Examples:
> (number->string (flonum->bit-field -inf.0) 16) "fff0000000000000"
> (number->string (flonum->bit-field +inf.0) 16) "7ff0000000000000"
> (number->string (flonum->bit-field -0.0) 16) "8000000000000000"
> (number->string (flonum->bit-field 0.0) 16) "0"
> (number->string (flonum->bit-field -1.0) 16) "bff0000000000000"
> (number->string (flonum->bit-field 1.0) 16) "3ff0000000000000"
> (number->string (flonum->bit-field +nan.0) 16) "7ff8000000000000"
procedure
(bit-field->flonum i) → flonum?
i : (integer-in 0 (- (expt 2 64) 1))
The inverse of flonum->bit-field.
procedure
(flonum->ordinal x)
→ (integer-in (- (- (expt 2 63) 1)) (- (expt 2 63) 1)) x : flonum?
Returns the signed ordinal index of x in a total order over flonums.
When inputs are not +nan.0, this function is monotone and symmetric;
i.e. if (fl<= x y) then (<= (flonum->ordinal x) (flonum->ordinal y)),
and (= (flonum->ordinal (- x)) (- (flonum->ordinal x))).
Examples:
> (flonum->ordinal -inf.0) -9218868437227405312
> (flonum->ordinal +inf.0) 9218868437227405312
> (flonum->ordinal -0.0) 0
> (flonum->ordinal 0.0) 0
> (flonum->ordinal -1.0) -4607182418800017408
> (flonum->ordinal 1.0) 4607182418800017408
> (flonum->ordinal +nan.0) 9221120237041090560
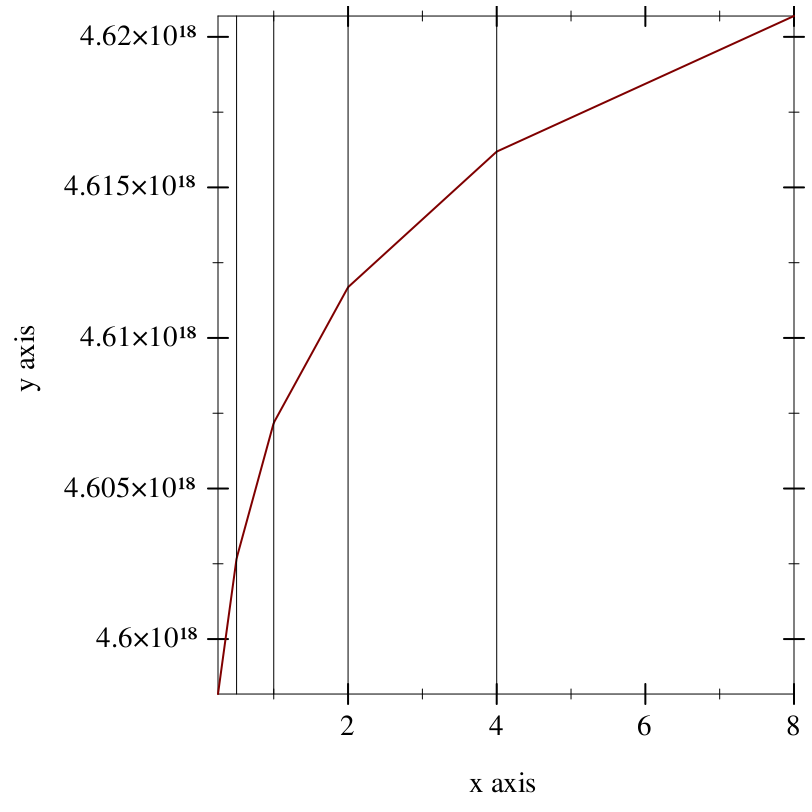
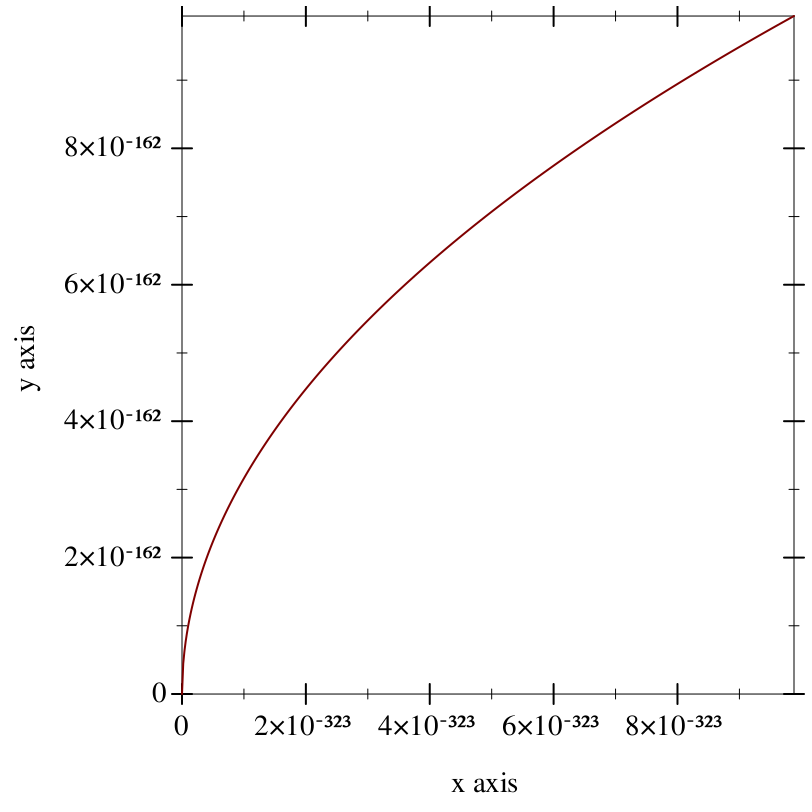
The following plot demonstrates how the density of floating-point numbers decreases with magnitude:
Example:
> (parameterize ([y-axis-ticks? #f]) (plot (list (function (compose flonum->ordinal exact->inexact) 1/4 8) (y-axis 1/2) (y-axis 1) (y-axis 2) (y-axis 4))))
procedure
(ordinal->flonum i) → flonum?
i : (integer-in (- (- (expt 2 63) 1)) (- (expt 2 63) 1))
The inverse of flonum->ordinal.
procedure
(flonums-between x y) → exact-integer?
x : flonum? y : flonum?
Returns the number of flonums between x and y, excluding one endpoint.
Equivalent to (- (flonum->ordinal y) (flonum->ordinal x)).
Examples:
> (flonums-between 0.0 1.0) 4607182418800017408
> (flonums-between 1.0 2.0) 4503599627370496
> (flonums-between 2.0 3.0) 2251799813685248
> (flonums-between 1.0 +inf.0) 4611686018427387904
procedure
x : flonum? n : exact-integer?
Returns the flonum n flonums away from x, according to flonum->ordinal. If x is +nan.0, returns +nan.0.
Examples:
The rational flonums with maximum and minimum magnitude.